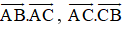Giải toán 10: Phần Hình học: Chương 2: Tích vô hướ...
- Câu 1 : Tam giác ABC vuông tại A có góc nhọn (ABC) ̂ = α. Hãy nhắc lại định nghĩa các tỉ số lượng giác của góc nhọn α đã học ở lớp 9.
- Câu 2 : Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O nằm phía trên trục hoành bán kính R = 1 được gọi là nửa đường tròn đơn vị (h.2.2). Nếu cho trước một góc nhọn α thì ta có thể xác định một điểm M duy nhất trên nửa đường tròn đơn vị sao cho ∠(xOM) = α. Giả sử điểm M có tọa độ (xo; yo).
- Câu 3 : Tìm các giá trị lượng giác của các góc 120o, 150o.
- Câu 4 : Chứng minh rằng trong tam giác ABC có:
- Câu 5 : Cho AOB là tam giác cân tại O có OA = a và có các đường cao OH và AK. Giả sử ∠AOH = α. Tính AK và OK theo a và α.
- Câu 6 : Chứng minh rằng với mọi góc a (0o ≤ a ≤ 180o) ta đều có cos2+ sin2α = 1.
- Câu 7 : Cho góc x, với cosx = 1/3. Tính giá trị của biểu thức: P = 3sin2x + cos2x.
- Câu 8 : Cho hình vuông ABCD. Tính
- Câu 9 : Cho hai vectơ a→ và b→đều khác 0→. Khi nào thì tích vô hướng của hai vectơ đó là số dương ? Là số âm ? Bằng 0 ?
- Câu 10 : Trên mặt phẳng tọa độ Oxy cho ba điểm A(2; 4), B(1; 2), C(6; 2). Chứng minh AB→ ⊥ AC→.
- Câu 11 : Cho tam giác vuông cân ABC có AB = AC = a. Tính các tích vô hướng
- Câu 12 : Cho ba điểm O, A, B thẳng hàng và biết OA = a, OB = b. Tính tích vô hướng
trong hai trường hợp:
- Câu 13 : Cho nửa hình tròn tâm O có đường kính AB=2R. Gọi M và N là hai điểm thuộc nửa đường tròn sao cho hai dây cung AM và BN cắt nhau tại I.
- Câu 14 : Trên mặt phẳng Oxy, cho hai điểm A(1; 3), B(4; 2).
- Câu 15 : Trên mặt phẳng Oxy hãy tính góc giữa hai vectơ a→ và b→ trong các trường hợp sau:
- Câu 16 : Trên mặt phẳng tọa độ Oxy cho bốn điểm: A(7; -3), B(8; 4), C(1; 5), D(0; –2). Chứng minh rằng tứ giác ABCD là hình vuông.
- Câu 17 : Trên mặt phẳng Oxy cho điểm A(-2; 1). Gọi B là điểm đối xứng với điểm A qua gốc tọa độ O. Tìm tọa độ của điểm C có tung độ bằng 2 sao cho tam giác vuông ở C.
- Câu 18 : Tam giác ABC vuông tại A có đường cao AH = h và có BC = a, CA = b, AB = c. Gọi BH = c’ và CH = b’(h.2.11). Hãy điền vào các ô trống trong các hệ thức sau đây để được các hệ thức lượng trong tam giác vuông:
- Câu 19 : Hãy phát biểu định lí cosin bằng lời
- Câu 20 : Khi ABC là tam giác vuông, định lý côsin trở thành định lý quen thuộc nào?
- Câu 21 : Cho tam giác ABC có a = 7cm, b = 8cm, c = 6cm. Hãy tính độ dài đường trung tuyến ma của tam giác ABC đã cho.
- Câu 22 : Cho tam giác ABC vuông ở A nội tiếp trong đường tròn bán kính R và có BC = a, CA = b, AB = c.
- Câu 23 : Cho tam giác đều ABC có cạnh bằng a. Hãy tính bán kính đường tròn ngoại tiếp tam giác đó.
- Câu 24 : Hãy viết các công thức tính diện tích tam giác theo một cạnh và đường cao tương ứng.
- Câu 25 : Dựa vào công thức (1) và định lý sin, hãy chứng minh S = abc/4R.
- Câu 26 : Chứng minh công thức S = pr
- Câu 27 : Cho tam giác ABC vuông tại A, B̂ = 58o và cạnh a = 72cm. Tính Ĉ, cạnh b và đường cao ha.
- Câu 28 : Cho tam giác ABC biết các cạnh a = 52,1cm, b = 85cm, c = 54cm. Tính các góc Â, B̂, Ĉ.
- Câu 29 : Cho tam giác ABC có Â = 120o, cạnh b = 8cm và c = 5cm. Tính cạnh a, các góc B̂, Ĉ của tam giác đó.
- Câu 30 : Tính diện tích S của tam giác có số đo các cạnh lần lượt là 7, 9 và 12.
- Câu 31 : Cho tam giác ABC có Â = 120o. Tính cạnh BC, cho biết cạnh AC = m và cạnh AB = n.
- Câu 32 : Tam giác ABC có các cạnh a = 8cm, b = 10cm và c = 13cm.
- Câu 33 : Tính góc lớn nhất của tam giác ABC biết:
- Câu 34 : Cho tam giác ABC biết cạnh a = 137,5cm, ∠B = 83o và ∠C = 57o. Tính góc A, bán kính R của đường tròn ngoại tiếp, cạnh b và c của tam giác.
- Câu 35 : Cho hình bình hành ABCD có AB = a, BC = b, BD = m, AC = n. Chứng minh rằng: m2 + n2 = 2(a2 + b2).
- Câu 36 : Hai chiếc tàu thủy P và Q cách nhau 300m. Từ P và Q thẳng hàng với chân A của tháp hải đăng AB ở trên bờ biển người ra nhìn chiều cao AB của tháp dưới các góc ∠BPA = 35o và ∠BQA = 48o. Tính chiều cao của tháp.
- Câu 37 : Muốn đo chiều cao của Tháp Chàm Por Klong Garai ở Ninh Thuận, người ta lấy hai điểm A và B trên mặt đất có khoảng cách AB = 12 m cùng thẳng hàng với chân C của tháp để đặt hai giác kế (hình bên). Chân của giác kế có chiều cao h = 1,3m. Gọi D là đỉnh tháp và hai điểm A1, B1 cùng thẳng hàng với C1 thuộc chiều cao CD của tháp. Người ta đo được ∠DA1C1 = 49o và ∠DB1C1 = 35o. Tính chiều cao CD của tháp đó.
- Câu 38 : Hãy nhắc lại định nghĩa giá trị lượng giác của một góc α với 0o ≤ α ≤ 180o. Tại sao khi α là các góc nhọn thì giá trị lượng giác này lại chính là các tỉ số lượng giác đã được học ở lớp 9?
- Câu 39 : Tại sao hai góc bù nhau lại có sin bằng nhau và cos đối nhau?
- Câu 40 : Nhắc lại định nghĩa tích vô hướng của hai vectơ a→ và b→. Tích vô hướng này với |a→| và |b→| không đổi đạt giá trị lớn nhất và nhỏ nhất khi nào?
- Câu 41 : Trong mặt phẳng Oxy cho vectơ a→(-3; 1) và b→(2; 2). Hãy tính tích vô hướng a→.b→.
- Câu 42 : Hãy nhắc lại định lí côsin trong tam giác. Từ các hệ thức này hãy tính cosA, cosB, cosC theo các cạnh của tam giác.
- Câu 43 : Từ hệ thức a2 = b2 + c2 - 2bc.cosA trong tam giác, hãy suy ra định lý Pi-ta-go.
- Câu 44 : Chứng minh rằng với mọi tam giác ABC, ta có a = 2RsinA, b = 2RsinB, c = 2RsinC, trong đó R là bán kính đường tròn ngoại tiếp tam giác.
- Câu 45 : Trong tam giác ABC. Chứng minh rằng
- Câu 46 : Cho tam giác ABC có góc A = 60o, BC = 6. Tính bán kính đường tròn ngoại tiếp tam giác đó
- Câu 47 : Cho tam giác ABC có a = 12, b = 16, c = 20. Tính diện tích S của tam giác, chiều cao ha, bán kính R, r của các đường tròn ngoại tiếp, nội tiếp tam giác và đường trung tuyến ma của tam giác
- Câu 48 : Trong tập hợp các tam giác có hai cạnh là a và b, tìm tam giác có diện tích lớn nhất.
Xem thêm
- - Trắc nghiệm Hình học 10 Bài 1 Các định nghĩa
- - Trắc nghiệm Hình học 10 Bài 2 Tổng và hiệu của hai vectơ
- - Trắc nghiệm Hình học 10 Bài 3 Tích của vectơ với một số
- - Trắc nghiệm Hình học 10 Bài 4 Hệ trục tọa độ
- - Trắc nghiệm Ôn tập chương Vectơ - Hình học 10
- - Trắc nghiệm Hình học 10 Bài 1 Giá trị lượng giác của một góc bất kỳ từ 0 độ đến 180 độ
- - Trắc nghiệm Hình học 10 Bài 2 Tích vô hướng của hai vectơ
- - Trắc nghiệm Hình học 10 Bài 3 Các hệ thức lượng trong tam giác và giải tam giác
- - Trắc nghiệm Ôn tập chương Tích vô hướng của hai vectơ và ứng dụng - Hình học 10
- - Trắc nghiệm Toán 10 Bài 1 Mệnh đề