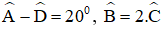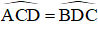Giải toán 8: Chương 1: Tứ giác !!
- Câu 1 : Trong các tứ giác ở hình 1, tứ giác nào luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của tứ giác ?
- Câu 2 : Quan sát tứ giác ABCD ở hình 3 rồi điền vào chỗ trống:
- Câu 3 : Tìm x ở hình 5, hình 6:
- Câu 4 : Góc kề bù với một góc của tứ giác gọi là góc ngoài của tứ giác.
- Câu 5 : Ta gọi tứ giác ABCD trên hình 8 có AB = AD, CB = CD là hình "cái diều".
- Câu 6 : Dựa vào cách vẽ các tam giác đã học, hãy vẽ lại các tứ giác ở hình 9, hình 10 vào vở.
- Câu 7 : Đố em tìm thấy vị trí của "kho báu" trên hình 11, biết rằng kho báu nằm tại giao điểm các đường chéo của tứ giác ABCD, trong đó các đỉnh của tứ giác có tọa độ như sau: A(3; 2), B(2; 7), C(6; 8), D(8; 5).
- Câu 8 : Cho hình 15.
- Câu 9 : Hình thang ABCD có đáy AB, CD.
- Câu 10 : Dùng thước và êke, ta có thể kiểm tra được hai đường thẳng có song song với nhau hay không (xem hình 19). Trên hình 20, có những tứ giác là hình thang, có những tứ giác không là hình thang. Bằng cách nêu trên, hãy kiểm tra xem trong các tứ giác ở hình 19, tứ giác nào là hình thang?
- Câu 11 : Tìm x và y trên hình 21, biết rằng ABCD là hình thang có đáy là AB và CD.
- Câu 12 : Hình thang ABCD (AB // CD) có
- Câu 13 : Tứ giác ABCD có AB = BC và AC là tia phân giác của góc A. Chứng minh rằng ABCD là hình thang.
- Câu 14 : Hình 12 là hình vẽ một chiếc thang. Trên hình vẽ có bao nhiêu hình thang?
- Câu 15 : Cho hình 24.
- Câu 16 : Cho đoạn thẳng CD và đường thẳng m song song với CD (h.29). Hãy vẽ các điểm A, B thuộc m sao cho ABCD là hình thang có hai đường chéo CA, DB bằng nhau. Sau đó hãy đo các góc C ̂ và D ̂ của hình thang ABCD đó để dự đoán về dạng của các hình thang có đường chéo bằng nhau.
- Câu 17 : Tính độ dài các cạnh của hình thang cân ABCD trên giấy kẻ ô vuông (h.30, độ dài của cạnh ô vuông là 1cm).
- Câu 18 : Cho hình thang cân ABCD (AB // CD, AB < CD). Kẻ các đường cao AE, BF của hình thang. Chứng minh rằng DE = CF.
- Câu 19 : Cho hình thang cân ABCD (AB//CD), E là giao điểm của hai đường chéo. Chứng minh rằng EA = EB, EC = ED.
- Câu 20 : Trong các tứ giác ABCD, EFGH trên giấy kẻ ô vuông (h.31), tứ giác nào là hình thang cân? Vì sao?
- Câu 21 : Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy theo thứ tự các điểm D, E sao cho AD = AE
- Câu 22 : Cho tam giác ABC cân tại A, các đường phân giác BD, CE (D ∈ AC, E ∈ AB). Chứng minh rằng BEDC là hình thang cân có đáy nhỏ bằng cạnh bên.
- Câu 23 : Hình thang ABCD (AB // CD) có
- Câu 24 : Chứng minh định lý: "Hình thang có hai đường chéo bằng nhau là hình thang cân" qua bài toán sau: Cho hình thang ABCD (AB // CD) có AC = BD. Qua B kẻ đường thẳng song song với AC, cắt đường thẳng DC tại tại E. Chứng minh rằng:
- Câu 25 : Cho ba điểm A, D, K trên giấy kẻ ô vuông (h.32) Hãy tìm điểm thứ tư M giao điểm của các dòng kẻ sao cho nó cùng với ba diểm đã cho là bốn đỉnh của một hình thang cân.
- Câu 26 : Vẽ tam giác ABC bất kì rồi lấy trung điểm D của AB. Qua D vẽ đường thẳng song song với BC, đường thẳng này cắt AC ở E. Bằng quan sát, hãy nêu dự đoán về vị trí của điểm E trên cạnh AC.
- Câu 27 : Vẽ tam giác ABC bất kì rồi lấy trung điểm D của AB, trung điểm E của AC. Dùng thước đo góc và thước chia khoảng để kiểm tra rằng ∠(ADE) = ∠B và DE = 1/2BC.
- Câu 28 : Tính độ dài đoạn BC trên hình 33.
- Câu 29 : Cho hình thang ABCD (AB // CD). Qua trung điểm E của AD kẻ đường thẳng song song với hai đáy, đường thẳng này cắt AC ở I, cắt BC ở F (h.37). Có nhận xét gì về vị trí của điểm I trên AC, điểm F trên BC ?
- Câu 30 : Tính x trên hình 40.
- Câu 31 : Tính x trên hình 41.
- Câu 32 : Tính khoảng cách AB giữa hai mũi của compa trên hình 42, biết rằng C là trung điểm của OA, D là trung điểm của OB và CD = 3cm.
- Câu 33 : Cho hình 43. Chứng minh rằng AI = IM.
- Câu 34 : Tìm x trên hình 44.
- Câu 35 : Hai điểm A và B thuộc cùng một nửa mặt phẳng có bờ là đường thẳng xy. Khoảng cách từ điểm A đến xy bằng 12cm, khoảng cách từ điểm B đến xy bằng 20cm. Tính khoảng cách từ trung điểm C của AB đến xy.
- Câu 36 : Hình thang ABCD có đáy AB, CD. Gọi E, F, K theo thứ tự là trung điểm của AD, BC, BD. Chứng minh ba điểm E, K, F thẳng hàng.
- Câu 37 : Tính x, y trên hình 45 trong đó AB // CD // EF // GH.
- Câu 38 : Cho tứ giác ABCD. Gọi E, F, K theo thứ tự là trung điểm của AD, BC, AC.
- Câu 39 : Cho hình thang ABCD (AB // CD), E là trung điểm của AD, F là trung điểm của BC. Đường thẳng EF cắt BD tại I, cắt AC ở K.
- Câu 40 : Dựng tam giác ABC vuông tại A, biết cạnh huyền BC = 4cm, góc nhọn B = 65o.
- Câu 41 : Dựng tam giác ABC vuông tại B, biết cạnh huyền AC = 4cm, cạnh góc vuông BC = 2cm.
- Câu 42 : Dựng hình thang ABCD (AB // CD), biết AB = AD = 2cm, AC = DC = 4cm.
- Câu 43 : Hãy dựng một góc bằng 30o.
- Câu 44 : Dựng hình thang cân ABCD, biết đáy CD = 3cm, đường chéo AC = 4cm, góc ∠D = 80o.
- Câu 45 : Dựng hình thang ABCD, biết ∠D = 90o, đáy CD = 3cm, cạnh bên AD = 2cm, cạnh bên BC = 3cm.
- Câu 46 : Cho đường thẳng d và một điểm A không thuộc d. Hãy vẽ điểm A’ sao cho d là đường trung trực của đoạn thẳng AA’.
- Câu 47 : Cho đường thẳng d và đoạn thẳng AB (h.51).
- Câu 48 : Cho tam giác ABC cân tại A, đường cao AH (h.55). Tìm hình đối xứng với mỗi cạnh của tam giác ABC qua AH.
- Câu 49 : Mỗi hình sau có bao nhiêu trục đối xứng ?
- Câu 50 : Vẽ hình đối xứng với các hình đã cho qua trục d (h.58).
- Câu 51 : Cho góc xOy có số đo 50o, điểm A nằm trong góc đó. Vẽ điểm B đối xứng với A qua Ox, vẽ điểm C đối xứng với A qua Oy.
- Câu 52 : Tìm các hình có trục đối xứng trên hình 59.
- Câu 53 : Cắt một tấm bìa hình tam giác cân, một tấm bìa hình thang cân. Hãy cho biết đường nào là trục đối xứng của mỗi hình, sau đó gấp mỗi tấm bìa để kiểm tra lại điều đó.
- Câu 54 : a) Cho hai điểm A, B thuộc cùng một mặt phẳng có bờ là đường thẳng d (h.60). Gọi C là điểm đối xứng với A qua d. Gọi D là giao điểm của đường thẳng d và đoạn thẳng BC. Gọi E là điểm bất kì của đường thẳng d (E khác D).
- Câu 55 : Trong các biển báo giao thông sau đây, biển nào có trục đối xứng?
- Câu 56 : Các cạnh đối của tứ giác ABCD trên hình 66 có gì đặc biệt?
- Câu 57 : Cho hình bình hành ABCD (h.67). Hãy thử phát hiện tính chất về cạnh, về góc, về đường chéo của hình bình hành đó.
- Câu 58 : Trong các tứ giác ở hình 70, tứ giác nào là hình bình hành? Vì sao?
- Câu 59 : Các tứ giác ABCD, EFGH, MNPQ trên giấy kẻ ô vuông ở hình 71 có là hình bình hành hay không?
- Câu 60 : Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC. Chứng minh rằng BE = DF
- Câu 61 : Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB ở E, tia phân giác của góc B cắt CD ở F.
- Câu 62 : Cho hình 72. Trong đó ABCD là hình bình hành
- Câu 63 : Tứ giác ABCD có E, F , G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì? Vì sao?
- Câu 64 : Cho hình bình hành ABCD. Gọi I, K theo thứ tự là trung điểm của CD, AB. Đường chéo BD cắt AI, CK theo thứ tự ở M và N. Chứng minh rằng:
- Câu 65 : Cho điểm O và điểm A. Hãy vẽ điểm A’ sao cho O là trung điểm của đoạn thẳng AA’.
- Câu 66 : Cho điểm O và đoạn thẳng AB (h.75)
- Câu 67 : Gọi O là giao điểm hai đường chéo của hình bình hành ABCD (h.79). Tìm hình đối xứng với mỗi cạnh của hình bình hành qua điểm O.
- Câu 68 : Trên hình 80, các chữ cái N và S có tâm đối xứng, chữ cái E không có tâm đối xứng. Hãy tìm thêm một vài chữ cái khác (kiểu chữ in hoa) có tâm đối xứng.
- Câu 69 : Vẽ điểm A' đối xứng với A qua B, vẽ điểm C' đối xứng với C qua B (h.81)
- Câu 70 : Trong mặt phẳng tọa độ, cho điểm H có tọa độ (3; 2). Hãy vẽ điểm K đối xứng với H qua gốc tọa độ và tìm tọa độ của K.
- Câu 71 : Cho hình bình hành ABCD. Gọi E là điểm đối xứng với D qua điểm A, gọi F là điểm đối xứng với D qua C. Chứng minh rằng E đối xứng với điểm F qua điểm B.
- Câu 72 : Cho hình 82, trong đó MD // AB và ME // AC. Chứng minh rằng điểm A đối xứng với điểm M qua điểm I.
- Câu 73 : Cho góc vuông xOy, điểm A nằm trong góc đó. Gọi B là điểm đối xứng với A qua Ox, gọi C là điểm đối xứng với A qua Oy. Chứng minh rằng điểm B đối xứng với điểm C qua O.
- Câu 74 : Cho hình bình hành ABCD, O là giao điểm của hai đường chéo. Một đường thẳng đi qua O cắt các cạnh AB và CD theo thứ tự ở M và N. Chứng minh rằng điểm M đối xứng với điểm N qua O.
- Câu 75 : Trong các hình sau, hình nào có tâm đối xứng?
- Câu 76 : Chứng minh rằng hình chữ nhật ABCD trên hình 84 cũng là một hình bình hành, một hình thang cân.
- Câu 77 : Với một chiếc compa, ta sẽ kiểm tra được hai đoạn thẳng bằng nhau hay không bằng nhau. Bằng compa, để kiểm tra tứ giác ABCD có là hình chữ nhật hay không, ta làm thế nào ?
- Câu 78 : Cho hình 86:
- Câu 79 : Cho hình 87:
- Câu 80 : Điền vào chỗ trống, biết rằng a, b là độ dài của các cạnh, d là độ dài đường chéo của một hình chữ nhật.
- Câu 81 : Chứng minh rằng:
- Câu 82 : Tính độ dài đường trung tuyến ứng với cạnh huyền của một tam giác vuông có cạch góc vuông bằng 7cm và 24 cm.
- Câu 83 : Cho tam giác ABC, đường cao AH. Gọi I là trung điểm của AC, E là điểm đối xứng với H qua I. Tứ giác AHCE là hình gì? Vì sao?
- Câu 84 : Tìm x trên hình 90
- Câu 85 : Cho hình bình hành ABCD. Các tia phân giác của các góc A, B, C, D cắt nhau như trên hình 91. Chứng minh rằng EFGH là hình chữ nhật.
- Câu 86 : Tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì? Vì sao?
- Câu 87 : Một đội công nhân đang trồng cây trên đoạn đường AB thì gặp chướng ngại vật che lấp tầm nhìn (h.92). Đội đã dựng các điểm C, D, E như trên hình vẽ rồi trồng cây tiếp trên đoạn đường EF vuông góc với DE. Vì sao AB và EF cùng nằm trên một đường thẳng?
- Câu 88 : Cho hai đường thẳng song song a và b (h.93).
- Câu 89 : Cho đường thẳng b. Gọi a và a’ là hai đường thẳng song song với đường thẳng b và cùng cách đường thẳng b một khoảng bằng h (h.94), (I) và (II) là các nửa mặt phẳng bờ b. Gọi M, M’ là các điểm cách đường thẳng b một khoảng bằng h, trong đó M thuộc nửa mặt phẳng (I), M’ thuộc nửa mặt phẳng (II). Chứng minh rằng M ∈ a, M’ ∈ a’.
- Câu 90 : Xét các tam giác ABC có BC cố định, đường cao ứng với cạnh BC luôn bằng 2 cm (h.95). Đỉnh A của các tam giác đó nằm trên đường nào?
- Câu 91 : Cho hình 96b, trong đó các đường thẳng a, b, c, d song song với nhau.
- Câu 92 : Cho đoạn thẳng AB. Kẻ tia Ax bất kì. Trên tia Ax lấy các điểm C, D, E sao cho AC = CD = DE (h.97). Kẻ đoạn thẳng EB. Qua C, D kẻ các đường thẳng song song với EB. Chứng minh rằng đoạn thẳng AB bị chia ra ba phần bằng nhau.
- Câu 93 : Cho điểm A nằm ngoài đường thẳng d và có khoảng cách đến d bằng 2cm. Lấy điểm B bất kì thuộc đường thẳng d. Gọi C là điểm đối xứng với điểm A qua điểm B. Khi điểm B di chuyển trên đường thẳng d thì điểm C di chuyển trên đường nào?
- Câu 94 : Ghép mỗi ý (1), (2), (3), (4) với một trong các ý (5), (6), (7), (8) để được một khẳng định đúng.
- Câu 95 : Cho góc vuông xOy, điểm A thuộc tia Oy sao cho OA = 2cm. Lấy B là một điểm bất kì thuộc tia Ox. Gọi C là trung điểm của AB. Khi điểm B di chuyển trên tia Ox thì điểm C di chuyển trên đường nào?
- Câu 96 : Cho tam giác ABC vuông tại A. Lấy M là một điểm bất kì thuộc cạnh BC. Gọi MD là đường vuông góc kẻ từ M đến AB, ME là đường vuông góc kẻ từ M đến AC, O là trung điểm của DE.
- Câu 97 : Để vạch một đường thẳng song song với mép gỗ AB và cách mép gỗ 10cm, bác thợ mộc đặt đoạn bút chì CD dài 10cm vuông góc với ngón tay trỏ lấy làm cữ (h.98), rồi đưa ngón trỏ chạy dọc theo mép gỗ AB. Căn cứ vào kiến thức nào mà ta kết luận rằng đầu chì C vạch nên đường thẳng song song với AB và cách AB là 10cm?.
- Câu 98 : Chứng minh rằng tứ giác ABCD trên hình 100 cũng là một hình bình hành.
- Câu 99 : Cho hình thoi ABCD, hai đường chéo cắt nhau tại O (h.101).
- Câu 100 : Hãy chứng minh dấu hiệu nhận biết 3.
- Câu 101 : Tìm các hình thoi trên hình 102.
- Câu 102 : Hai đường chéo của một hình thoi bằng 8cm và 10cm. Cạnh của hình thoi bằng giá trị nào trong các giá trị sau:
- Câu 103 : Chứng minh rằng các trung điểm của bốn cạnh của một hình chữ nhật là các đỉnh của một hình thoi.
- Câu 104 : Chứng minh rằng các trung điểm của bốn cạnh của một hình thoi là các đỉnh của một hình chữ nhật.
- Câu 105 : Hình 103 biểu diễn một phần của cửa xếp, gồm những thanh kim loại dài bằng nhau và được liên kết với nhau bởi các chốt tại hai đầu và tại trung điểm. Vì sao tại mỗi vị trí của cửa xếp, các tứ giác trên hình vẽ đều là hình thoi, các điểm chốt I, K, M, N, O nằm trên một đường thẳng?
- Câu 106 : Đường chéo của hình vuông có những tính chất gì?
- Câu 107 : Tìm các hình vuông trên hình 105.
- Câu 108 : a) Một hình vuông có cạnh bằng 3cm. Đường chéo của hình vuông đó bằng: 6cm, √18 cm, 5cm hay 4cm?
- Câu 109 : Hãy chỉ rõ tâm đối xứng của hình vuông, các trục đối xứng của hình vuông.
- Câu 110 : Cho hình 106. Tứ giác AEDF là hình gì? Vì sao?
- Câu 111 : Cho hình 107, trong đó ABCD là hình vuông. Chứng minh rằng tứ giác EFGH là hình vuông.
- Câu 112 : Cho tam giác ABC, D là điểm nằm giữa B và C. Qua D kẻ các đường thẳng song song với AB và AC, chúng cắt các cạnh AC và AB theo thứ tự ở E và F.
- Câu 113 : Cho hình chữ nhật ABCD có AB = 2AD. Gọi E, F theo thứ tự là trung diểm của AB, CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE.
- Câu 114 : Lấy một tờ giấy gấp làm tư rồi cắt chéo theo nhát cắt AB (h.108). Sau khi mở tờ giấy ra, ta được một tứ giác. Tứ giác nhận được là hình gì? Vì sao? Nếu ta có OA = OB thì tứ giác nhận được là hình gì?
- Câu 115 : Phát biểu định nghĩa tứ giác.
- Câu 116 : Phát biểu định nghĩa hình thang, hình thang cân.
- Câu 117 : Phát biểu các tính chất của hình thang cân.
- Câu 118 : Phát biểu các tính chất của đường trung bình của tam giác, đường trung bình của hình thang.
- Câu 119 : Phát biểu định nghĩa hình bình hành, hình chữ nhật, hình thoi, hình vuông.
- Câu 120 : Phát biểu các tính chất của hình bình hành, hình chữ nhật, hình thoi, hình vuông.
- Câu 121 : Nêu các dấu hiệu nhận biết hình bình hành, hình chữ nhật, hình thoi, hình vuông.
- Câu 122 : Thế nào là hai điểm đối xứng với nhau qua một đường thẳng? Trục đối xứng của hình thang cân là đường thẳng nào?
- Câu 123 : Thế nào là hai điểm đối xứng với nhau qua một điểm? Tâm đối xứng của hình bình hành là điểm nào?
- Câu 124 : Sơ đồ ở hình 109 biểu thị quan hệ giữa các tập hợp hình thang, hình bình hành, hình chữ nhật, hình thoi, hình vuông. Dựa vào sơ đồ đó, hãy điền vào chỗ trống:
- Câu 125 : Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA. Các đường chéo AC, BD của tứ giác ABCD có điều kiện gì thì EFGH là:
- Câu 126 : Cho tam giác ABC vuông tại A, đường trung tuyến AM. Gọi D là trung điểm của AB, E là điểm dối xứng với M qua D.
- Câu 127 : Tìm trục đối xứng và tâm đối xứng của:
Xem thêm
- - Trắc nghiệm Toán 8 Bài 1 Liên hệ giữa thứ tự và phép cộng
- - Trắc nghiệm Bài 2 Liên hệ giữa thứ tự và phép nhân - Luyện tập - Toán 8
- - Trắc nghiệm Toán 8 Bài 1 Nhân đơn thức với đa thức
- - Trắc nghiệm Hình học 8 Bài 1 Tứ giác
- - Trắc nghiệm Toán 8 Bài 2 Nhân đa thức với đa thức
- - Trắc nghiệm Toán 8 Bài 3 Những hằng đẳng thức đáng nhớ
- - Trắc nghiệm Toán 8 Bài 4 Những hằng đẳng thức đáng nhớ (tiếp)
- - Trắc nghiệm Toán 8 Bài 5 Những hằng đẳng thức đáng nhớ (tiếp)
- - Trắc nghiệm Toán 8 Bài 6 Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
- - Trắc nghiệm Toán 8 Bài 7 Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức