Cho hình lập phương \(ABCD.A'B'C'D'\) cạnh \(a\)....
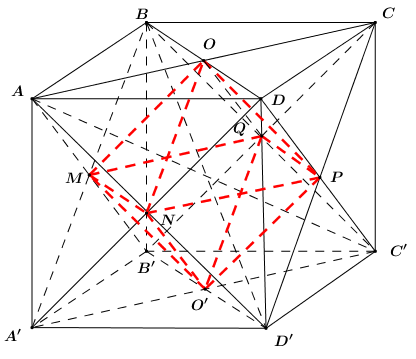
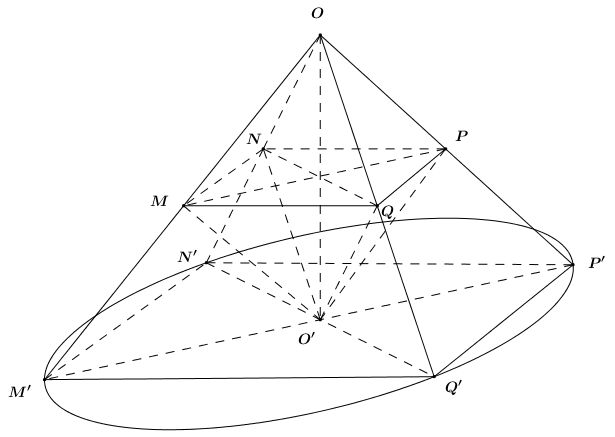
Câu hỏi: Cho hình lập phương \(ABCD.A'B'C'D'\) cạnh \(a\). Gọi \(O,\,\,O'\) lần lượt là tâm của hai đáy \(ABCD\) và \(A'B'C'D'\). Xét khối đa diện \(\left( H \right)\) có các điểm bên trong là phần không gian chung của hai khối tứ diện \(ACB'D'\) và \(A'C'BD\). Gọi \({V_1}\) là thể tích của phần không gian bên trong hình lập phương không bị \(\left( H \right)\) chiếm chỗ, \({V_2}\) là thể tích khối nón \(\left( N \right)\) đi qua tất cả các đỉnh của đa diện \(\left( H \right)\), đỉnh và tâm đáy của \(\left( N \right)\) lần lượt là \(O,\,\,O'\). Tính \(\dfrac{{{V_1}}}{{{V_2}}}\).
A \(\dfrac{{{V_1}}}{{{V_2}}} = \dfrac{2}{{5\pi }}\)
B \(\dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{2\pi }}{5}\)
C \(\dfrac{{{V_1}}}{{{V_2}}} = \dfrac{5}{{2\pi }}\)
D \(\dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{5\pi }}{2}\)
Câu hỏi trên thuộc đề trắc nghiệm
40 bài tập trắc nghiệm mặt nón mức độ vận dụng, vận dung cao