Cho hình lập phương \(ABCD.A'B'C'D'\) có thể tích...
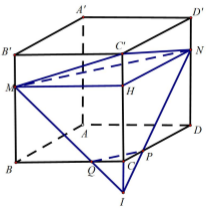
Câu hỏi: Cho hình lập phương \(ABCD.A'B'C'D'\) có thể tích \(V\). Gọi \(M\) là điểm thuộc cạnh \(BB'\) sao cho \(MB = 2MB'\). Mặt phẳng \(\left( \alpha \right)\) đi qua \(M\) và vuông góc với \(AC'\) cắt các cạnh \(DD'\), \(DC\), \(BC\) lần lượt tại \(N\), \(P\), \(Q\). Gọi \({V_1}\) là thể tích của khối đa diện \(CPQMNC'\).Tính tỉ số \(\dfrac{{{V_1}}}{V}\).
A \(\dfrac{{31}}{{162}}\)
B \(\dfrac{{35}}{{162}}\)
C \(\dfrac{{34}}{{162}}\)
D \(\dfrac{{13}}{{162}}\)
Câu hỏi trên thuộc đề trắc nghiệm
20 bài tập trắc nghiệm thể tích khối đa diện mức độ vận dụng cao