Cho ngũ giác đều ABCDE. Gọi M, N, P, Q,, R t...
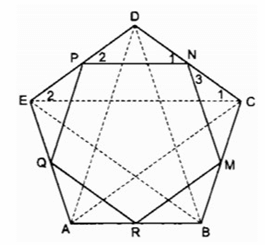
Câu hỏi: Cho ngũ giác đều ABCDE. Gọi M, N, P, Q,, R tương ứng là trung điểm của các cạnh BC, CD, DE, EA, AB. Chứng minh MNPQR là ngũ giác đều.
Đáp án
- Hướng dẫn giải
Xét ABC và BCD:
AB = BC (gt)
B = C (gt)
BC = CD (gt)
Do đó: ABC = BCD (c.g.c)
⇒ AC = BD (1)
Xét BCD và CDE:
BC = CD (gt)
C = D (gt)
CD = DE (gt)
Do đó: BCD = CDE (c.g.c) ⇒ BD = CE (2)
Xét CDE và DEA:
CD = DE (gt)
D = E (gt)
DE = EA (gt)
Do đó: CDE = DEA (c.g.c) ⇒ CE = DA (3)
Xét DEA và EAB:
DE = EA (gt)
E = A (gt)
EA = AB (gt)
Do đó: DEA = EAB (c.g.c) ⇒ DA = EB (4)
Từ (1), (2), (3), (4) suy ra: AC = BD = CE = DA = EB
Trong ABC ta có RM là đường trung bình
⇒ RM = 1/2 AC (tính chất đường trung bình của tam giác)
Mặt khác, ta có: Trong Δ BCD ta có MN là đường trung bình
⇒ MN = 1/2 BD (tính chất đường trung bình của tam giác)
Trong CDE ta có NP là đường trung bình
⇒ NP = 1/2 CE (tính chất đường trung bình của tam giác)
Trong DEA ta có PQ là đường trung bình
⇒ PQ = 1/2 DA (tính chất đường trung bình của tam giác)
Trong EAB ta có QR là đường trung bình
⇒ QR = 1/2 EB (tính chất đường trung bình của tam giác)
Suy ra: MN = NP = PQ = QR = RM
Ta có: A = B = C = D = E = ((5-2 ).)/5 =
DPN cân tại D
⇒ (DPN) = (DNP) = (- D )/2 = ( - )/2 =
CNM cân tại C
⇒ (CNM) = (CMN) = (- D )/2 = ( - )/2 =
(ADN) + (PNM) + (CNM) =
⇒ (PNM) = - ((ADN) + (CNM) )
= - ( – ) =
BMR cân tại B
⇒ (BMR) = (BRM) = (- B )/2 = ( - )/2 =
(CMN) + (BRM) + (BMR) =
⇒ (NMR) = - ((CMN) + (BMR) )
= - ( – ) =
ARQ cân tại A
⇒ (ARQ) = (AQR) = (- A )/2 = ( - )/2 =
(BRM) + (MRQ) + (ARQ) =
⇒ (MRQ) = - ((BRM) + (ARQ) )
= - ( – ) =
QEP cân tại E
⇒ (EQP) = (EPQ) = (- E )/2 = ( - )/2 =
(AQR) + (RQP) + (EQP) =
⇒ (RQP) = - ((AQR) + (EQP) )
= - ( – ) =
(EQP) + (QPN) + (DPN) =
⇒ (QPN) = - ((EPQ) + (DPN) )
= - ( – ) =
Suy ra : (PNM) = (NMR) = (MRQ) = (RQP) = (QPN)
Vậy MNPQR là ngũ giác đều.
Câu hỏi trên thuộc đề trắc nghiệm
Giải Sách Bài Tập Toán 8 Tập 1 !!