Cho khối chóp tứ giác đều \(S.ABCD\) có cạnh đáy b...
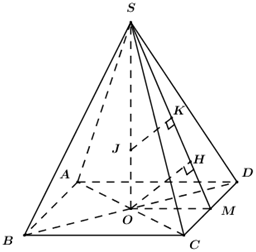
Câu hỏi: Cho khối chóp tứ giác đều \(S.ABCD\) có cạnh đáy bằng \(a\) và có thể tích \(V = \dfrac{{{a^3}\sqrt 3 }}{6}\). Tìm số \(r > 0\) sao cho tồn tại điểm \(J\) nằm trong khối chóp mà khoảng cách từ \(J\) đến các mặt bên và mặt đáy đều bằng \(r\)?
A \(r = \dfrac{{a\sqrt 3 }}{4}\)
B \(r = \dfrac{{a\sqrt 3 }}{2}\)
C \(r = \dfrac{{a\sqrt 3 }}{3}\)
D \(r = \dfrac{{a\sqrt 3 }}{6}\)
Câu hỏi trên thuộc đề trắc nghiệm
20 bài tập trắc nghiệm thể tích khối đa diện mức độ vận dụng cao