Cho

- Hướng dẫn giải

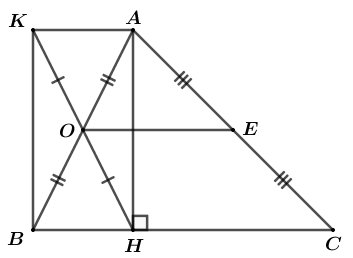
a) Chứng minh: OE // BC

Xét tam giác ABC có:

O là trung điểm của AB

E là trung điểm của AC

=> OE là đường trung bình của tam giác ABC

=> OE // BC (định lý đường trung bình trong tam giác)

b) Từ A vẽ  $\mathrm{AH}\perp \mathrm{BC}$ tại H. Gọi K là điểm đối xứng của H qua O. Chứng minh tứ giác AHBK là hình chữ nhật.

Vì K là điểm đối xứng của H qua O nên O là trung điểm của HK.

Xét tứ giác AHBK ta có:

O là trung điểm của HK

O là trung điểm của AB

O là giao điểm của đường chéo HK và AB.

Suy ra, tứ giác AHBK là hình bình hành (dấu hiệu nhận biết)

Mặt khác, $\mathrm{AH}\perp \mathrm{BC}$ tại H nên $\widehat{\mathrm{AHB}}={90}^{\circ }$

=> Tứ giác AHBK là hình chữ nhật (dấu hiệu nhận biết)

c) Giả sử BA = BC. Chứng minh $\mathrm{EH}\perp \mathrm{EK}$.

Theo câu a) ta có OE là đường trung bình của tam giác ABC.

$\Rightarrow \mathrm{OE}=\frac{1}{2}\mathrm{BC}$ mà $\mathrm{BA}=\mathrm{BC}\Rightarrow \mathrm{OE}=\frac{1}{2}\mathrm{BA}$ (1)

Ta lại có: AHBK là hình chữ nhật nên AB = HK (tính chất của hình chữ nhật)

$\Rightarrow \mathrm{OK}=\mathrm{OH}=\frac{1}{2}\mathrm{KH}=\frac{1}{2}\mathrm{BA}$ (2)

Từ (1) và (2) suy ra: OE = OK = OH

Ta có:

+) OE = OK => $\mathrm{\Delta EOK}$ cân tại O (định nghĩa tam giác cân)

$\Rightarrow \widehat{\mathrm{OKE}}=\widehat{\mathrm{OEK}}$ (tính chất)

+) OE = OH => $\mathrm{\Delta EOH}$ cân tại O (định nghĩa tam giác cân)

$\Rightarrow \widehat{\mathrm{OHE}}=\widehat{\mathrm{OEH}}$ (tính chất)

Xét tam giác EKH ta có:

$\widehat{\mathrm{HKE}}+\widehat{\mathrm{KEH}}+\widehat{\mathrm{EHK}}={180}^{\circ }$ (định lý tổng ba góc trong một tam giác)

$\Rightarrow \widehat{\mathrm{OKE}}+\widehat{\mathrm{OEK}}+\widehat{\mathrm{OHE}}+\widehat{\mathrm{OEH}}={180}^{\circ }$

$\Rightarrow 2\left(\widehat{\mathrm{OEK}}+\widehat{\mathrm{OEH}}\right)={180}^{\circ }$

$\Rightarrow \widehat{\mathrm{OEK}}+\widehat{\mathrm{OEH}}={90}^{\circ }$

$\Rightarrow \widehat{\mathrm{KEH}}={90}^{\circ }$

$\Rightarrow \mathrm{EK}\perp \mathrm{EH}$ tại E