Cho tứ diện \(ABCD\) có \(G\) là điểm thỏa mãn \(\...

B

- Hướng dẫn giải

Lời giải chi tiết:

Gọi \(O\) là trọng tâm tam giác \(BCD\)

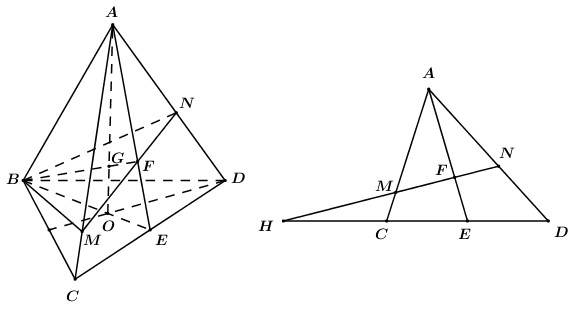
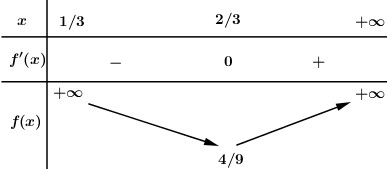
\(\begin{array}{l} \Rightarrow \overrightarrow {GB}  + \overrightarrow {GC}  + \overrightarrow {GD}  = 3\overrightarrow {GO} \\ \Rightarrow \overrightarrow {GA}  + 3\overrightarrow {GO}  = \overrightarrow 0 \\ \Rightarrow \overrightarrow {GA}  =  - 3\overrightarrow {GO} \\ \Rightarrow \dfrac{{AG}}{{AO}} = \dfrac{3}{4}\end{array}\)

Trong \(\left( {ABE} \right)\) gọi \(F = BG \cap AE\,\,\left( {F \in AE} \right)\).

Lấy \(M \in AC\), trong \(\left( {ACD} \right)\) gọi \(N = MF \cap AD\,\,\,\left( {N \in AD} \right)\), khi đó ta có mặt phẳng chứa \(BG\) cắt \(AC,\,\,AD\) lần lượt tại \(M,\,\,N\) chính là \(\left( {BMN} \right)\).

Áp dụng định lí Menelaus trong tam giác \(AOE\), cát tuyến \(BGF\):

\(\dfrac{{GA}}{{GO}}.\dfrac{{BO}}{{BE}}.\dfrac{{FE}}{{FA}} = 1 \Rightarrow 3.\dfrac{2}{3}.\dfrac{{FE}}{{FA}} = 1 \Rightarrow \dfrac{{FE}}{{FA}} = \dfrac{1}{2}\) \( \Rightarrow \dfrac{{AF}}{{AE}} = \dfrac{2}{3}\) \( \Rightarrow F\) là trọng tâm tam giác \(ACD\).

Trong \(\left( {ACD} \right)\) kéo dài \(MN\) cắt \(CD\) tại \(H\). Đặt \(\dfrac{{AM}}{{AC}} = x\) \(\left( {0 < x < 1} \right)\).

 Áp dụng định lí Menelaus trong tam giác \(ACE\), cát tuyến \(MHF\):

\(\dfrac{{MA}}{{MC}}.\dfrac{{HC}}{{HE}}.\dfrac{{FE}}{{FA}} = 1 \Rightarrow \dfrac{x}{{1 - x}}.\dfrac{{HC}}{{HE}}.\dfrac{1}{2} = 1\)\( \Rightarrow \dfrac{{HC}}{{HE}} = \dfrac{{2\left( {1 - x} \right)}}{x}\)

\(\begin{array}{l} \Rightarrow HE = \dfrac{x}{{2\left( {1 - x} \right)}}HC\\ \Rightarrow HC + CE = \dfrac{x}{{2\left( {1 - x} \right)}}HC\\ \Rightarrow CE = \dfrac{{3x - 2}}{{2\left( {1 - x} \right)}}HC\end{array}\)

Ta có:

\(\begin{array}{l}HD = HC + 2CE\\\,\,\,\,\,\,\,\,\, = HC + \dfrac{{3x - 2}}{{1 - x}}HC = \dfrac{{2x - 1}}{{1 - x}}HC\\ \Rightarrow \dfrac{{HE}}{{HD}} = \dfrac{x}{{2\left( {1 - x} \right)}}:\dfrac{{2x - 1}}{{1 - x}} = \dfrac{x}{{2\left( {2x - 1} \right)}}\end{array}\)

Áp dụng định lí Menelaus trong tam giác \(AED\), cát tuyến \(MFN\):

\(\begin{array}{l}\dfrac{{FA}}{{FE}}.\dfrac{{HE}}{{HD}}.\dfrac{{ND}}{{NA}} = 1 \Rightarrow 2.\dfrac{x}{{2\left( {2x - 1} \right)}}.\dfrac{{ND}}{{NA}} = 1\\ \Rightarrow \dfrac{{ND}}{{NA}} = \dfrac{{2x - 1}}{x} \Rightarrow \dfrac{{NA}}{{ND}} = \dfrac{x}{{2x - 1}}\\ \Rightarrow \dfrac{{NA}}{{NA + ND}} = \dfrac{x}{{x + 2x - 1}} = \dfrac{x}{{3x - 1}}\\ \Rightarrow \dfrac{{AN}}{{AD}} = \dfrac{x}{{3x - 1}}\end{array}\).

Khi đó ta có \(\dfrac{{{V_{ABMN}}}}{{{V_{ABCD}}}} = \dfrac{{AM}}{{AC}}.\dfrac{{AN}}{{AD}} = x.\dfrac{x}{{3x - 1}} = \dfrac{{{x^2}}}{{3x - 1}}\,\,\left( {x > \dfrac{1}{3}} \right)\).

Xét hàm số \(f\left( x \right) = \dfrac{{{x^2}}}{{3x - 1}}\,\,\left( {x > \dfrac{1}{3}} \right)\) ta có \(f'\left( x \right) = \dfrac{{2x\left( {3x - 1} \right) - 3{x^2}}}{{{{\left( {3x - 1} \right)}^2}}} = \dfrac{{3{x^2} - 2x}}{{{{\left( {3x - 1} \right)}^2}}}\); \(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\,\,\left( {ktm} \right)\\x = \dfrac{2}{3}\end{array} \right.\)

BBT:

Dựa vào BBT ta thấy \(\mathop {\min }\limits_{\left( {\frac{1}{3}; + \infty } \right)} f\left( x \right) = f\left( {\dfrac{2}{3}} \right) = \dfrac{4}{9}\).

Vậy giá trị nhỏ nhất của tỉ số \(\dfrac{{{V_{ABMN}}}}{{{V_{ABCD}}}} = \dfrac{4}{9}\).

Chọn B.