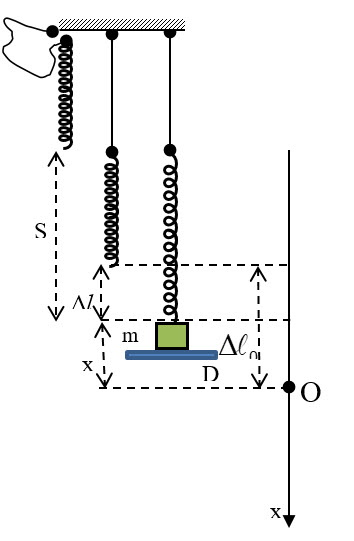
Cho cơ hệ như hình vẽ: lò xo rất nhẹ có độ cứng 10...
Câu hỏi: Cho cơ hệ như hình vẽ: lò xo rất nhẹ có độ cứng 100 N/m nối với vật m có khối lượng 1 kg , sợi dây rất nhẹ có chiều dài 2,5 cm và không giãn, một đầu sợi dây nối với lò xo, đầu còn lại nối với giá treo cố định. Vật m được đặt trên giá đỡ D và lò xo không biến dạng, lò xo luôn có phương thẳng đứng, đầu trên của lò xo lúc đầu sát với giá treo. Cho giá đỡ D bắt đầu chuyển động thẳng đứng xuống dưới nhanh dần đều với gia tốc có độ lớn là 5 m/s2. Bỏ qua mọi lực cản, lấy g = 10 m/s2. Biên độ dao động của m sau khi giá đỡ D rời khỏi nó là

A. 15 cm.
B. 7,5 cm.
C. 10 cm.
D. 20 cm.
Câu hỏi trên thuộc đề trắc nghiệm
Đề luyện thi THPT môn Lý lần 1 năm 2021 Trần Cao Vân (có đáp án)