Một con lắc lò xo được treo vào một điểm cố định đ...

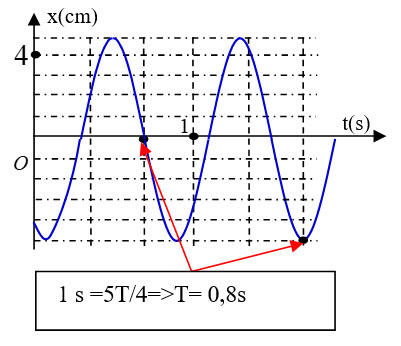
Câu hỏi: Một con lắc lò xo được treo vào một điểm cố định đang dao động điều hòa theo phương thẳng đứng. Hình bên là đồ thị biểu diễn sự phụ thuộc ly độ x của vật m theo thời gian t. Tần số dao động của con lắc lò xo có giá trị là

A. 1,5 Hz.

B. 1,25 Hz

C.0,5 Hz

D. 0,8 Hz

Đáp án

- Hướng dẫn giải

Mỗi ô có khoảng thời gian là 1/3 s
Từ đồ thị ta có 3 ô (từ ô thứ 2 đến ô thứ 5 có 5T/4 =1 s):
\[\dfrac{{5T}}{4} = 1s \Rightarrow T = 0,8s = > f = \dfrac{1}{T} = \dfrac{1}{{0,8}} = 1,25Hz.\]
Một con lắc lò xo được treo vào một điểm cố định đang dao động điều hòa theo hình ảnh 2

Một con lắc lò xo được treo vào một điểm cố định đang dao động điều hòa theo hình ảnh 2

Câu hỏi trên thuộc đề trắc nghiệm

Đề luyện thi THPT môn Lý lần 1 năm 2021 Trần Cao Vân (có đáp án)

↑